Участие в олимпиадах по информатике требует глубокого понимания не только основ программирования, но и эффективных способов обработки информации. Алгоритмы и структуры данных являются центральными элементами, на которых строится решение большинства задач. Умение выбирать подходящий алгоритм и правильно применять структуры данных позволяет значительно сократить время выполнения программы и повысить шансы на успешное выступление.
Важнейшие алгоритмы для олимпиад
Для успешного решения олимпиадных задач важно знать основные алгоритмы, которые часто встречаются в соревнованиях. К ним относятся сортировки, которые позволяют упорядочить данные для более удобной обработки, а также алгоритмы поиска, которые помогают эффективно находить нужную информацию в больших объемах данных. Кроме того, алгоритмы работы с графами, такие как обходы в глубину и ширину, играют ключевую роль в задачах, связанных с сетями и маршрутами.
Также большое значение имеют жадные алгоритмы и динамическое программирование, которые позволяют находить оптимальные решения в сложных ситуациях, разбивая задачу на более простые подзадачи. Знание и умение применять эти методы дает преимущество, так как многие задачи олимпиад построены именно на принципах оптимизации и эффективного поиска. Умение быстро переключаться между различными подходами и правильно выбирать алгоритм — залог успеха на олимпиаде.
Немаловажно и понимание теории сложностей алгоритмов, чтобы оценивать их эффективность и корректно применять в рамках ограниченного времени и ресурсов. Освоение этих алгоритмов не только помогает успешно проходить олимпиады, но и закладывает прочный фундамент для будущей профессиональной деятельности в области программирования и компьютерных наук.
Сложность алгоритмов и её анализ
Понимание сложности алгоритмов — ключевой момент для успешного решения олимпиадных задач. Сложность определяет, насколько эффективно алгоритм справится с обработкой больших объемов данных и сможет ли он уложиться в отведённое время. Обычно сложность выражают через обозначения вроде O(n), где n — размер входных данных. Эти оценки помогают заранее определить, будет ли алгоритм работать быстро и оптимально.
Анализ сложности позволяет сравнивать различные алгоритмы и выбирать наиболее подходящий для конкретной задачи. Например, алгоритм с квадратичной сложностью O(n²) может работать быстро на маленьких данных, но станет непригоден для больших. В таких случаях предпочтение отдают алгоритмам с линейной или логарифмической сложностью, которые обрабатывают информацию гораздо эффективнее.
Кроме того, важно понимать не только временную, но и пространственную сложность — количество памяти, которое потребует алгоритм. Оптимизация обоих параметров помогает добиться наилучших результатов в условиях ограниченных ресурсов. Таким образом, умение анализировать сложность — это не просто теоретический навык, а практическое средство для успешного решения олимпиадных задач и реальных задач программирования.
Структуры данных: массивы, списки, деревья
Структуры данных — фундамент программирования, без которых невозможно эффективно организовать и обрабатывать информацию. Массивы являются одной из самых простых и широко используемых структур. Они представляют собой набор элементов одинакового типа, расположенных в памяти подряд. Благодаря этому доступ к любому элементу осуществляется быстро и напрямую по индексу, что делает массивы удобными для хранения данных с фиксированным размером.
Списки, в отличие от массивов, позволяют динамически менять размер и удобно вставлять или удалять элементы в любом месте. Особенно популярны связные списки, где каждый элемент содержит указатель на следующий. Это обеспечивает гибкость при работе с данными, однако доступ к элементам не так быстр, как в массиве, так как приходится последовательно переходить от одного узла к другому.
Деревья — более сложная структура, часто применяемая для организации данных в иерархическом порядке. Они позволяют эффективно выполнять операции поиска, вставки и удаления благодаря особенностям своей структуры. Например, бинарные деревья поиска помогают быстро находить нужные элементы, что особенно важно для алгоритмов с большими объемами данных. Освоение этих структур — важный шаг к пониманию основ алгоритмики и успешному решению олимпиадных задач.
Как решать задачи на основе структур данных
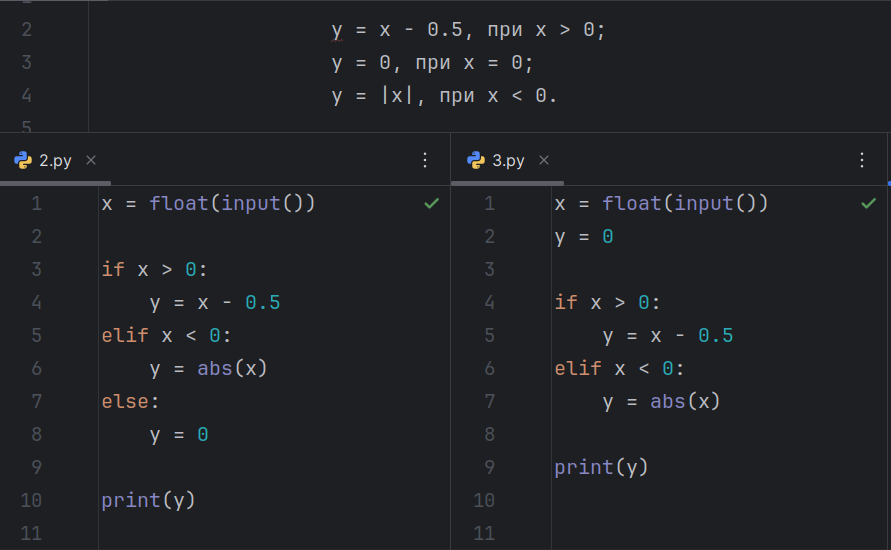
Для успешного решения задач на основе структур данных важно сначала чётко понять, какую структуру следует использовать в конкретной ситуации. Правильный выбор зависит от особенностей задачи: например, если требуется быстрый доступ по индексу, подойдут массивы, если важна динамическая вставка и удаление — списки, а для упорядоченного поиска — деревья. Осознание этих принципов помогает не тратить время на неэффективные подходы и ускоряет процесс решения.
Далее следует разобраться с основными операциями, которые необходимо выполнить над выбранной структурой. Это может быть поиск, сортировка, вставка или удаление элементов. Важно уметь не просто применять готовые алгоритмы, а понимать, как они работают и каким образом влияют на производительность решения. Анализ временной сложности помогает оценить, насколько эффективно будет работать программа при увеличении объёма данных.
Наконец, важно регулярно тренироваться на разнообразных задачах, чтобы научиться быстро распознавать паттерны и применять соответствующие структуры данных. Часто задачи олимпиад требуют комбинирования нескольких структур, поэтому умение интегрировать их вместе значительно расширяет возможности решения. Постепенно вырабатывая такую практику, можно значительно повысить уровень подготовки и успешно справляться с наиболее сложными вызовами.