Изучение алгоритмической сложности — важный этап в освоении программирования и решении задач на олимпиадах. Понимание того, как оценивается эффективность алгоритмов, помогает выбирать оптимальные решения и предсказывать их поведение на больших данных. Разбираясь в понятиях времени и памяти, можно создавать программы, которые работают быстрее и эффективнее. В этой статье рассмотрим основные подходы к изучению и применению анализа сложности.
Оценка сложности алгоритмов
Оценка сложности алгоритмов — ключевой навык для любого программиста, особенно тех, кто готовится к олимпиадам. Она помогает понять, сколько времени и памяти потребуется для выполнения конкретного решения при росте объёма входных данных. Обычно сложность выражается в виде функции, которая показывает, как изменяется время выполнения в зависимости от размера входа. Это позволяет сравнивать разные алгоритмы и выбирать наиболее эффективные.
Существуют разные типы сложности — временная и пространственная. Временная сложность показывает, сколько шагов нужно выполнить алгоритму, а пространственная — сколько памяти он потребляет. Важным инструментом здесь является нотация «O-большое», которая обобщает поведение алгоритма в худшем или среднем случае, позволяя сосредоточиться на главных факторах, влияющих на скорость работы.
Правильная оценка сложности помогает избежать излишне медленных решений и оптимизировать код, что особенно важно в условиях ограниченного времени и ресурсов на олимпиадах. Изучение этого аспекта открывает дорогу к более глубокому пониманию алгоритмических задач и позволяет уверенно справляться с вызовами любой сложности.
Классы сложности: P, NP, NP-полные задачи
Понимание классов сложности — важный шаг в изучении алгоритмики и теории вычислений. Класс P объединяет задачи, которые можно решить за полиномиальное время, то есть эффективность алгоритма растёт не слишком быстро при увеличении размера входных данных. Такие задачи считаются «легкими» для вычислений, и многие из них хорошо изучены и имеют эффективные решения.
В отличие от P, класс NP включает задачи, решения которых можно проверить за полиномиальное время, но не обязательно найти быстро. Это значит, что если у вас есть правильный ответ, вы можете быстро убедиться в его правильности, но найти этот ответ может быть намного сложнее. NP-класс объединяет множество важных задач, часто связанных с оптимизацией и комбинированием, которые сложно решать напрямую.
Особое место занимают NP-полные задачи — это подмножество NP, которое считается самым трудным. Если существует быстрый алгоритм для любой NP-полной задачи, то все задачи из NP будут решаться эффективно. Поэтому поиск решений для NP-полных задач — одна из центральных проблем информатики и математики. Понимание этих классов помогает ориентироваться в теории сложности и выбирать правильные подходы при решении сложных алгоритмических задач.
Как выбирать оптимальные алгоритмы для задач
Выбор оптимального алгоритма — ключевой этап в решении любой задачи, особенно в условиях ограниченного времени и ресурсов. Для начала важно оценить размер и тип входных данных, так как это напрямую влияет на производительность алгоритма. Например, алгоритмы с высокой временной сложностью могут быть приемлемы для небольших наборов данных, но окажутся непрактичными при масштабировании.
Также стоит учитывать структуру задачи: одни алгоритмы лучше подходят для сортировки и поиска, другие — для работы с графами или динамическим программированием. Понимание природы задачи помогает выбрать метод, который не только корректно решит проблему, но и сделает это эффективно. Иногда стоит пожертвовать простотой реализации ради скорости или наоборот — в зависимости от требований к решению.
Не менее важен анализ алгоритмической сложности — это позволяет предсказать, как быстро алгоритм справится с ростом объёма данных. Если задача требует частого обновления данных или быстрой реакции, предпочтение стоит отдавать алгоритмам с оптимальной временной и пространственной сложностью. В итоге умение выбирать подходящий алгоритм становится одним из важнейших навыков в программировании и подготовке к олимпиадам.
Примеры задач с анализом сложности
Рассмотрение конкретных задач с анализом алгоритмической сложности помогает лучше понять, как применять теорию на практике. Например, задача поиска элемента в отсортированном массиве часто решается с помощью бинарного поиска. Его временная сложность — O(log n), что делает этот алгоритм очень эффективным даже при больших объемах данных. Сравнивая это с линейным поиском, имеющим сложность O(n), становится очевидна выгода выбора правильного метода.
Другой пример — задача сортировки. Сортировка пузырьком проста в реализации, но обладает временной сложностью O(n²), что сильно ограничивает её применение на больших данных. В то же время алгоритмы быстрой сортировки или сортировки слиянием обеспечивают среднюю сложность O(n log n), что значительно улучшает производительность и позволяет работать с большими объемами информации.
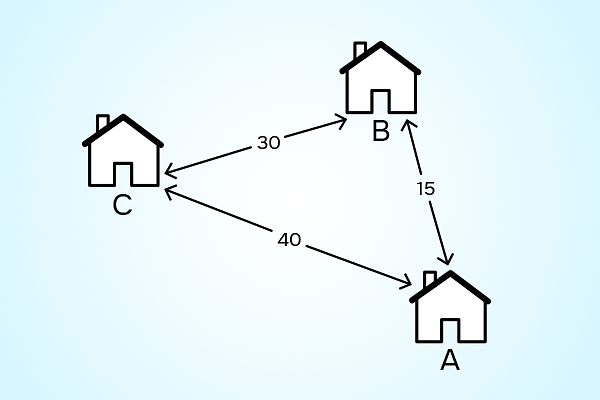
Задачи на графах также демонстрируют важность анализа сложности. Поиск в глубину (DFS) и поиск в ширину (BFS) имеют сложность O(V + E), где V — число вершин, а E — число рёбер. Это делает их пригодными для работы с разреженными графами. Однако более сложные алгоритмы, такие как алгоритм Дейкстры для поиска кратчайшего пути, требуют дополнительного анализа, чтобы оценить их эффективность в конкретных случаях и выбрать подходящий способ решения. Такие примеры показывают, что понимание алгоритмической сложности помогает не только ускорить работу программы, но и сделать её более устойчивой к росту данных.